목차는 아래와 같다.
논문에서 제안하는 핵심 method와 그에 대한 핵심 설명은 볼드체로 표기한다.
abstrct

데이터 부족과 컴퓨팅 파워의 효율성을 위해 few-shot-AD 그리고 fast reconstruction을 통해 pixel level로 anomal(쿼리) vs normal alignment(few-shot)를 맞춰 이상치를 탐지한다.
regression with distribution regularization을 제안하는데 이는 normal vs anomal의 alignment를 효과적으로 맞춰준다.
introduction
이전 연구는 특히, reconstruction based 그리고 feature bank L2loss compare 방법이 있었는데, 이는 많은 정상 이미지 그리고 높은 학습 비용에 의존한다.
연구자 왈 : real-world에서 "잘" 잘동하는 AD-model은 적은 데이터만 필요로 함. 그리고 빨라야 함.
그러기에 Fastrecon을 제안함. 이는 non-trainable, few-shot, fast 하기에 실제 산업 현장에서 사용될 수 있음.
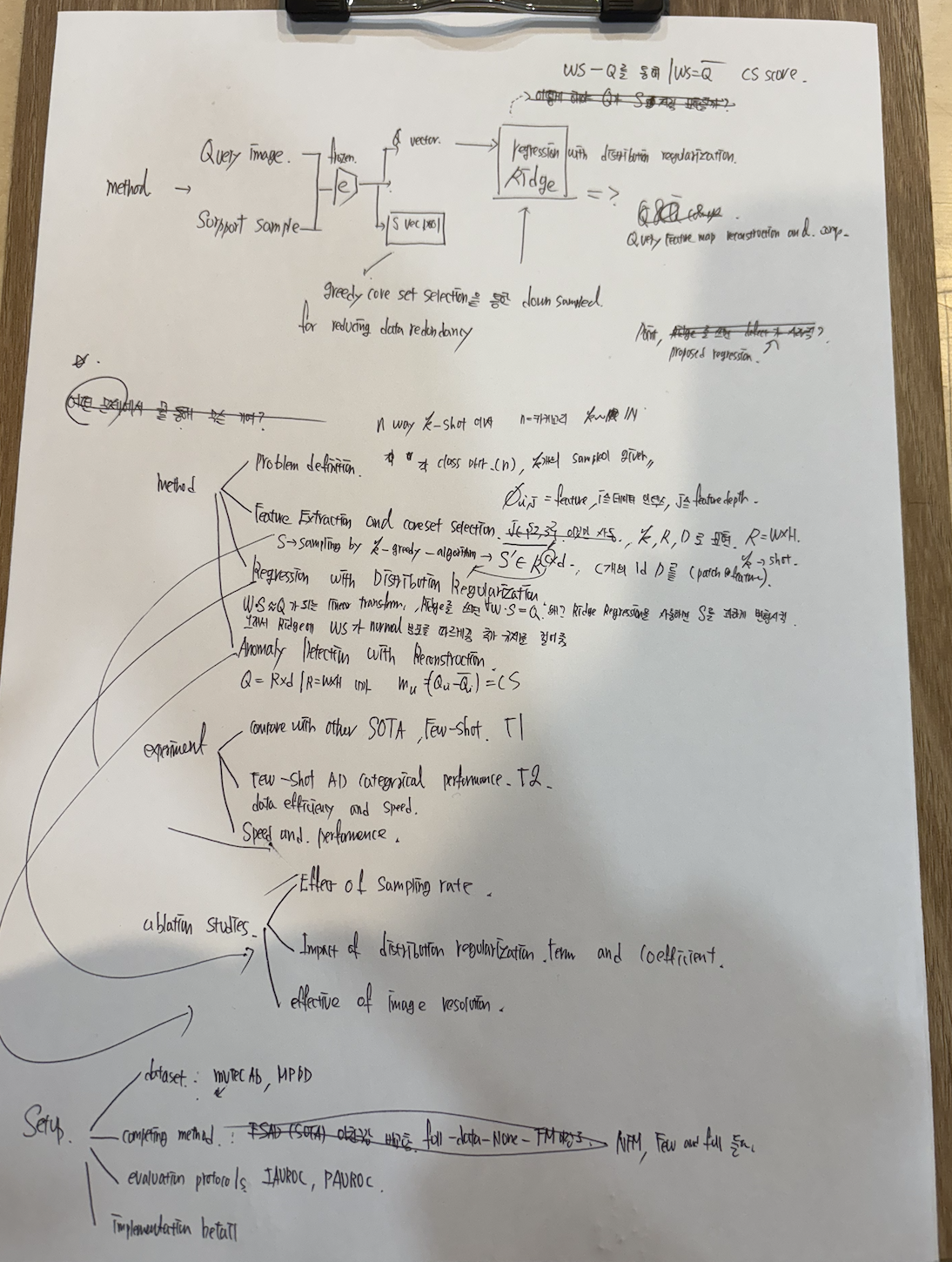
핵십은 optimal transformation을 찾는 것
여기서 말하는 optimal transformation은 정상 이미지들을 linear transform 시켜서 비정상 이미지와 비슷한 normal 이미지를 만드는 것이다. 위 그림에 상세히 나와있다.
아 이해했다. 정확히 요약해서 설명하자면,
1. 쿼리이미지랑(anomal) 정상 이미지가 있다고 가정하자.
2. 정상 이미지들을 조합해서 Q를 만들자. 그럼 defect가 있는 부분을 못 만들고 Q에서 defect가 빠진 모습의 이미지를 만들 것이다.
3. 그럼 원래 Q(anomal)랑 Q'(Q를 선형변환)을 서로 빼서, 차이가 심한지 확인한다. 차이가 심하면 해당 사진이 anomal이라 판단되는 것이다.
4. Q가 normal이라면, Q랑 Q'은 거의 동일한 이미지일 것이다.
MVTec, MDPP에서 AUROC기준 2, 4, 8-shot, full-shot SOTA를 달성함

method
feature extraction and coreset selection
- resnet-50을 사용하여 쿼리 이미지와 few-shot 이미지를 임베딩 한다.
- few-shot 이미지 임베딩 벡터는 POOL에 저장되는데 해당 POOL에서 데이터 중복을 줄이기 위해 K-greedy 알고리즘을 사용하여 최소 소의 피처를 남긴다.
regression with distribution regularization
- WS ~ Q | S = few-shot image, Q = query image
- W는 S를 linear transform 시키는 '커널'인데 그 결과로는 Q와 비슷한 분포를 갖는 벡터가 S의 linear combinatino으로 나온다.
- 해당 W를 찾는 과정에서 ridge 회귀를 사용하면 WS = Q가 되게 된다. WS~Q가 되어야 한다.

- Ridge회귀는 weight 규제를 거는 것이다. 즉, 커널을 근사하는 과정에는 규제가 생기지 않는다.
- 따라서 우리는 WS 가 normal image가 되기는 바라는데 정상 셈플의 linear transform으로 비정상 까지 만드니 WS랑 Q가 동일해져서 비교를 할 수 없다.

- 따라서 WS-Qterm이 노말 분포를 따르게 규제를 추가로 건다.
anomaly detection with recunstruction
위 과정을 따라오면 WS ~ Q가 되는데 WS는 무조건 정상 이미지이고, Q는 정상 or 비정상인 상태다.
1. WS - Q가 차이가 크면 -> Q는 비정상
2. WS == Q -> Q는 정상
expriment

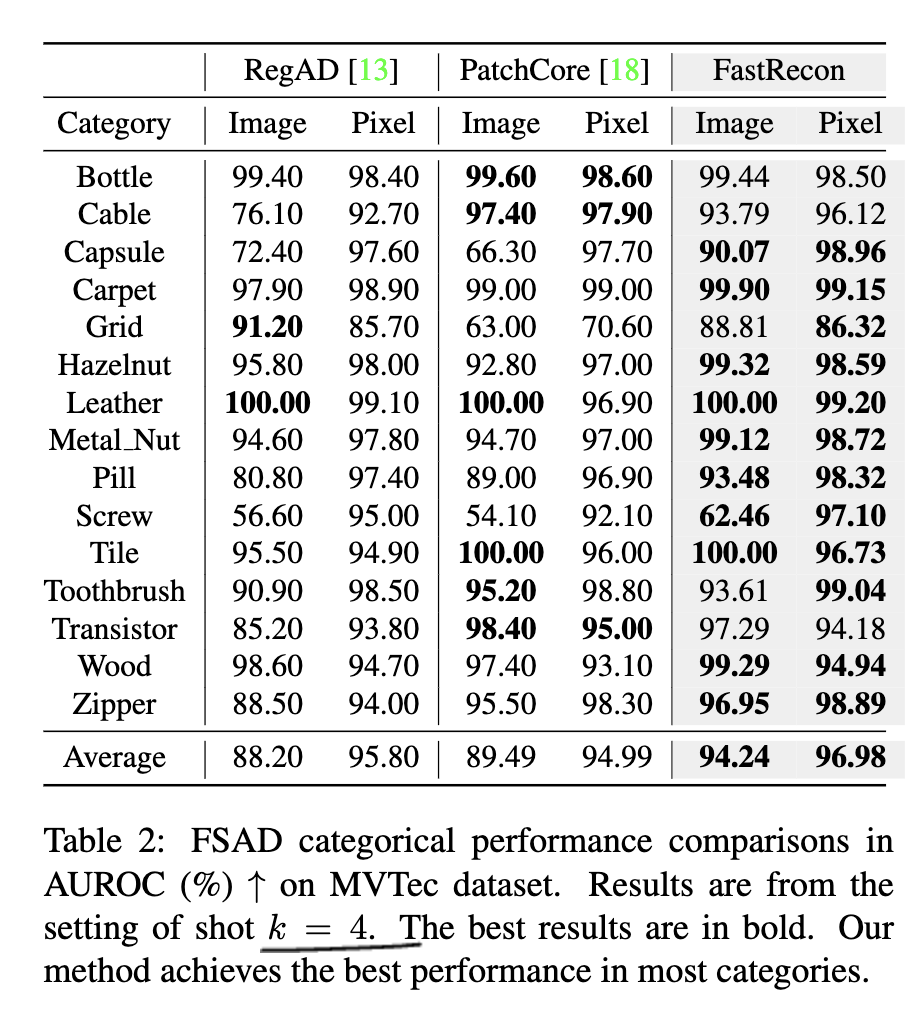

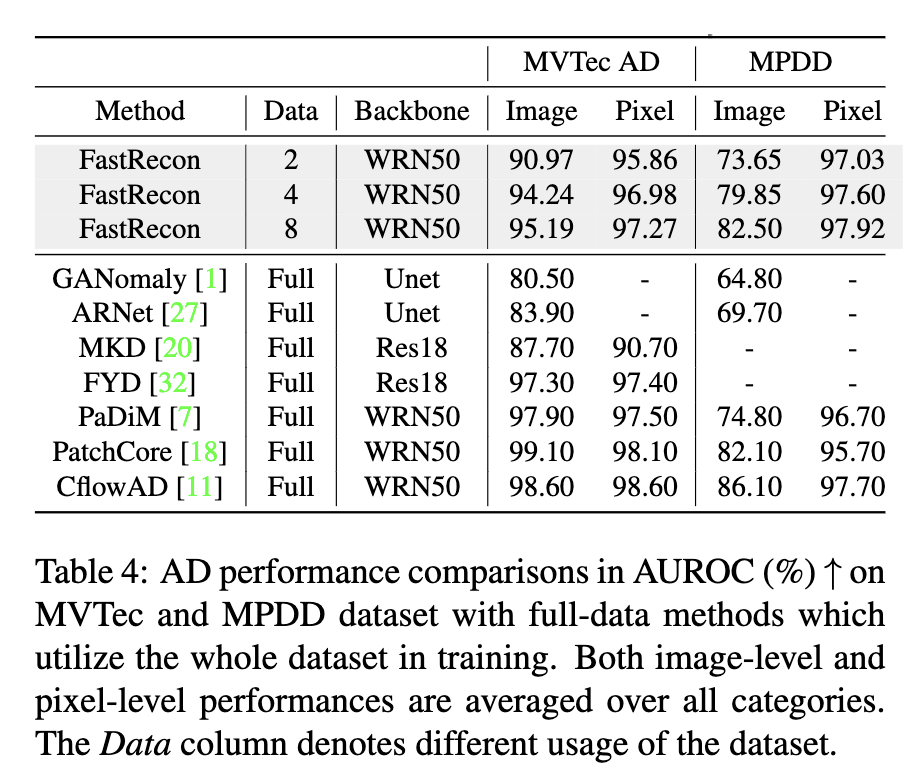
dataset
MVTec, MPPD 데이터를 전체 사용함
competing method
non-foundation-method-model들을 사용해서 full-shot, few-shot 둘 다 평가함.
evaluation protocols
image-level-AUROC, pixel-level-AUROC